Buongiorno,
come accennato a lezione mi domandavo se una mistura di gaussiane fosse davvero il miglior modello per attribuire i pesi alle diverse particelle del particle filter. Il dubbio mi è sorto quando provando tale modello nella pratica, nella porzione di percorso in cui si ha una sovrapposizione di 2 camera readings(chiamiamole "percorso1 vero"(fucsia) e "lettura intermittente 3"(giallo)), la probabilità associata a tale zona diventa troppo preponderante e va a deprivare quasi sempre del tutto le particelle che erano presenti su "percorso2 vero"(blu). Questo succede perché usando la mistura di gaussiane le probabilità si "sommano" (e poi ovviamente si normalizzano per avere una distribuzione di probabilità) e passo dopo passo a causa del resampling si converge verso la situazione descritta. Questo fenomeno non succedeva invece quando, come avevo pensato precedentemente, anziché utilizzare una mistura di gaussiane andavo a considerare solo la gaussiana più vicina alla singola particella. Facendo così infatti, il passaggio delle particelle dalla "zona critica" descritta prima era molto più robusto e il cluster su "percorso2 vero"(blu) non veniva deprivato eccessivamente.
Riassumendo:
- mistura di gaussiane PRIMA
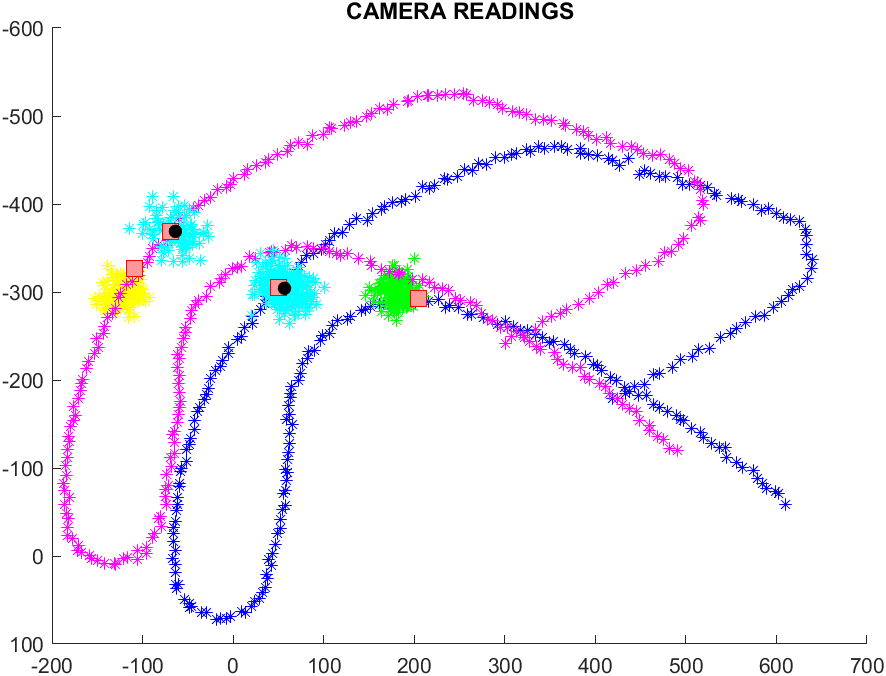
- mistura di gaussiane DOPO
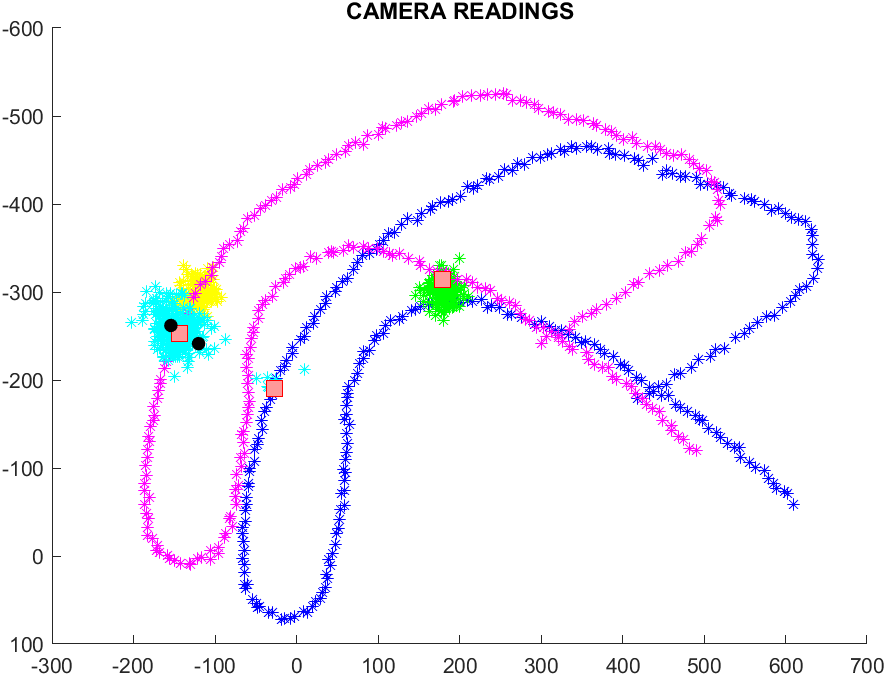
- gaussiana più vicina PRIMA
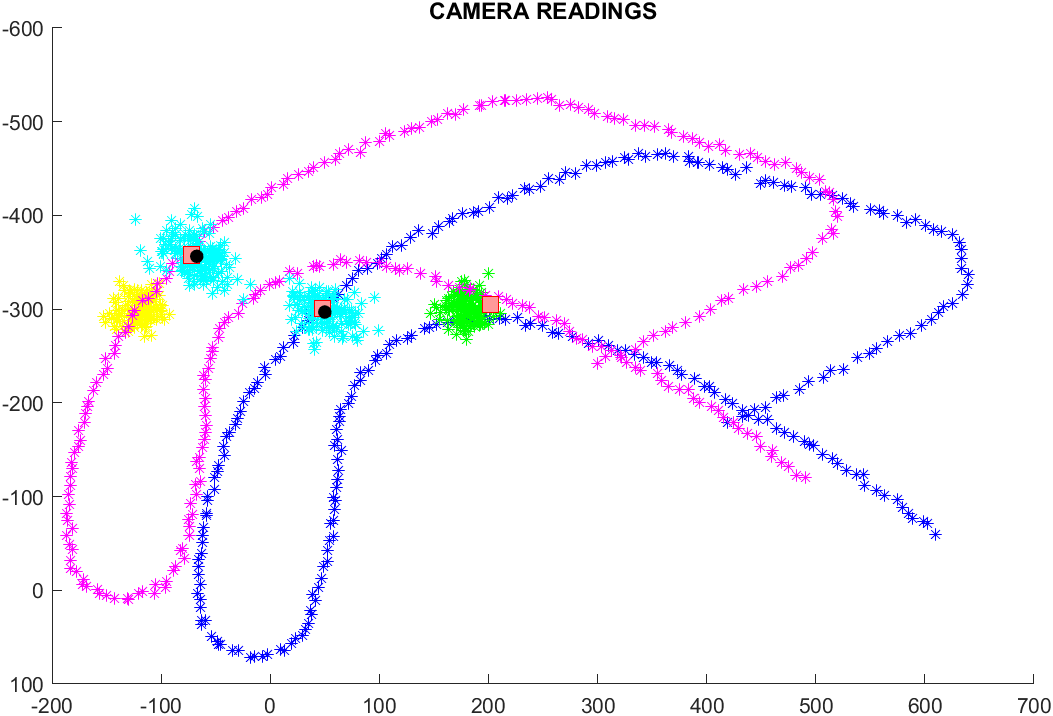
- gaussiana più vicina DOPO
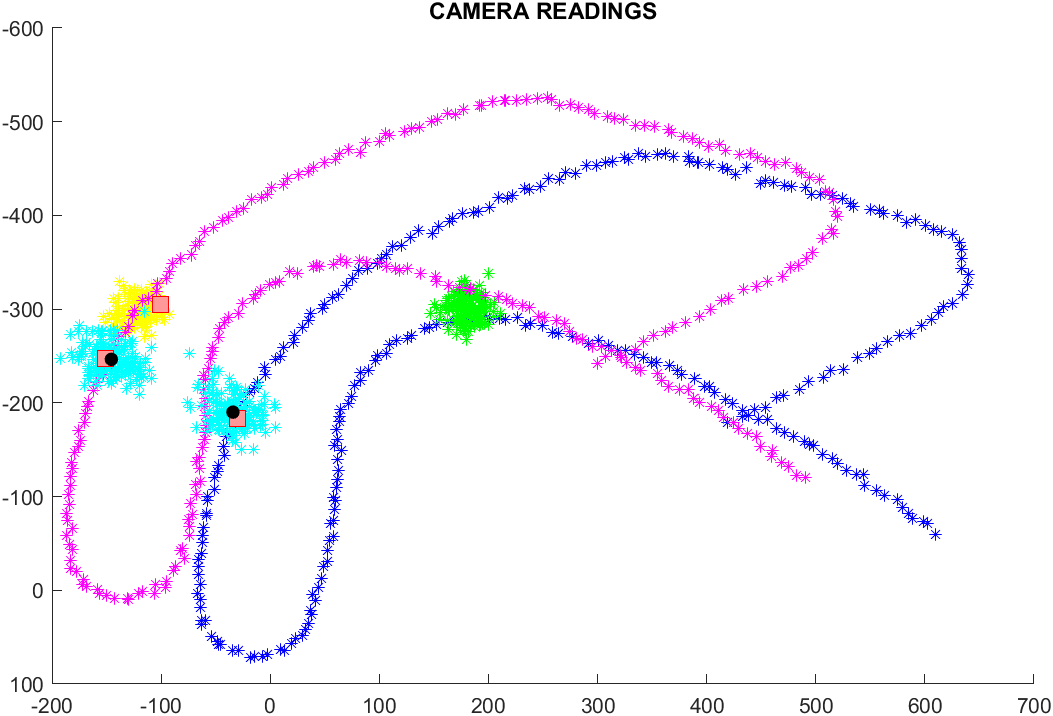
Generalizzando, per coprire anche i casi con gaussiane con incertezze differenti, si può dire che, mentre nella mistura viene effettuata una somma normalizzata delle diverse gaussiane, nel metodo descritto si va a prendere la funzione max(gussiana1, gaussiana2, ....), come nella seguente figura(la somma non è normalizzata), che rappresenta il caso 1D della situazione precedente:
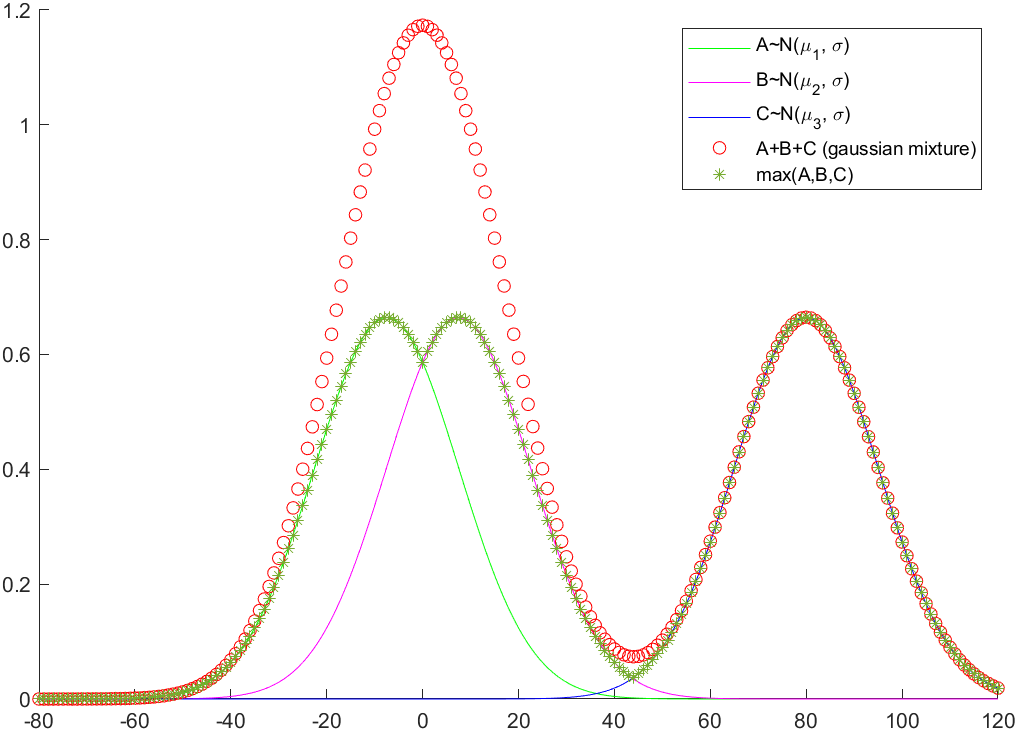
Si forza quindi a mantenere, in questo caso, 3 picchi nella distribuzione, poiché il numero di letture risulta 3 e si "scarica" il gioco delle probabilità non sull'altezza delle curve ma sull'estensione spaziale del dominio (tranne nel caso in cui le due gaussiane di sinistra risultano esattamente sovrapposte).
Il problema alternativamente potrebbe essere risolto andando ad impostare una incertezza delle gaussiane più piccola, in modo che le sovrapposizioni possibili si presentino solo nel caso in cui le camera readings siano davvero praticamente sovrapposte (poco probabile).
Specifico che tutto il discorso si basa sul fatto che si tenga conto solo delle letture del punto P1 del robot, e ci sono quindi dei possibili miglioramenti da fare che potrebbero portare il problema presentato a risolversi da solo, ma il discorso di base vale comunque in alcune istanze del problema generale.
