Gentile Ludovica,
per quanto riguarda gli esercizi li svolgerete con la tutor (Ilaria Castellano) durante le ore di esercitazione in sincrono (nel calendario sono indicate già le date e l'indirizzo Google Meet relativo).
Al termine delle esercitazioni relative verranno poi caricati anche i file con le soluzioni.
Nell'ultima delle videolezioni dell'unità faccio poi già un esempio di grafico di un'iperbole data la funzione relativa.
In ogni caso il procedimento generale è semplice e presto detto:
1. ricondurre la funzione alla forma \( \frac{ax+b}{cx+d} \).
Esempio: se si ha la funzione \( f(x) = 7\frac{x}{2(x+1)}-3 \) , occorre trasformarla come segue:
\( f(x) = 7\frac{x}{2(x+1)}-3 = \frac{7x-3(2x+2)}{2x+2}= \frac{x-6}{2x+2} \)
2. calcolare le coordinate del centro di simmetria C, sapendo che queste sono date da: \( (x_c,y_c) = (\frac{-d}{c}, \frac{a}{c}) \) e disegnare gli asintoti orizzontali e verticali dell'iperbole, che passano per questo punto.
Nel caso sopra si ha ad esempio che questo punto ha coordinate (-1,1/2).
3. dare un valore arbitrario ad x per ottenere il relativo valore di y, sapendo che uno dei rami dell'iperbole passerà per quel punto.Ed eventualmente altri valori di x più o meno "vicini" a quello per farsi un'idea migliore della curvatura del ramo dell'iperbole che si sta considerando.
Disegnare l'altro ramo dell'iperbole in modo simmetrico rispetto al centro di simmetria rispetto al primo.
A questo riguardo devi capire che, dato il centro di simmetria C, hai solo due possibilità perché i due rami dell'iperbole (perfettamente simmetrici rispetto agli assi di simmetria dell'iperbole) possono trovarsi:
i) o in alto a destra e in basso a sinistra,
ii) oppure in alto a sinistra e in basso a destra.
Calcolare un punto a caso ti permette di sapere in quale dei due casi ti trovi.
Per capire meglio quanto appena detto con un esempio, ecco i grafici delle seguenti due funzioni:
\( f(x) = \frac{x-6}{2x+2} \newline
g(x) = -\frac{x-6}{2x+2}+1 = \frac{x+8}{2x+2} \)
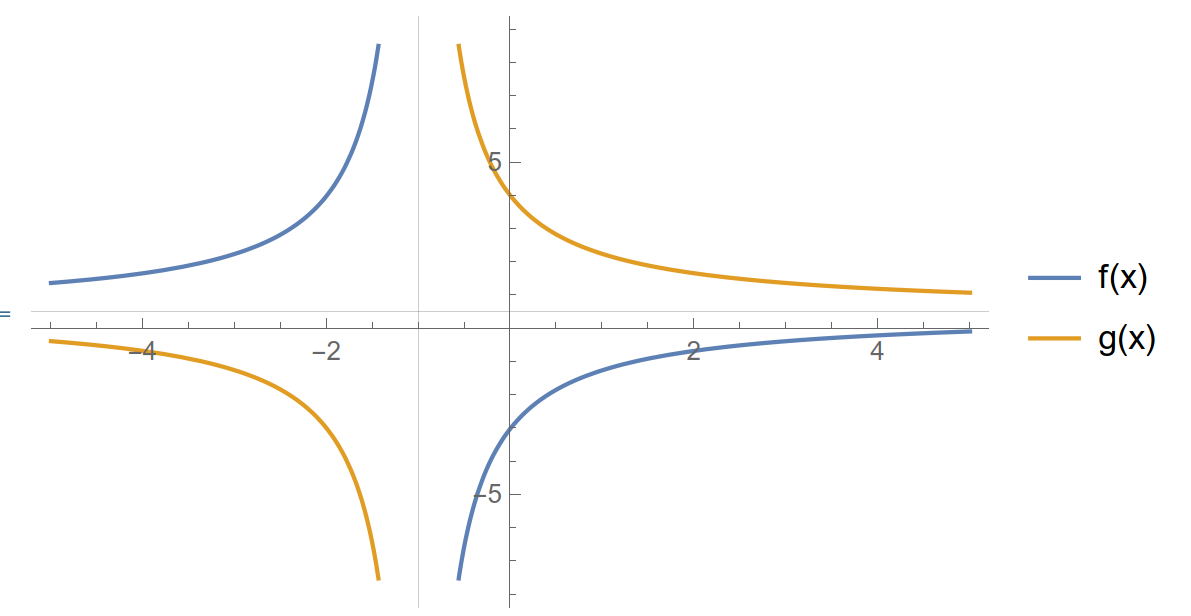
Come puoi vedere le due funzioni hanno restituito iperbole equilatere con stesso centro di simmetria e perfettamente identiche quanto a curvatura, ma i due casi sono distinti per la posizione dei relativi rami.
Spero di essere stato chiaro
Cordiali saluti
Giuseppe

