Buongiorno,
faccio un altro post perché ho diverse domande da fare, non necessariamente collegate all'argomento precedente.
1) Metodo per l'aggiornamento dei pesi:
Cercando informazioni online ho trovato il seguente algoritmo per l'aggiornamento dei pesi delle particelle di un particle filter, avendo a disposizione più misure:
N = numero di particelle
w(i+1) = p(xi | z)
p(xi | z) = (p(z | xi) * p(xi)) / p(z) % Teorema di Bayes
p(xi) = wi
p(z) = Σ[j=1,N] p(z | xj) * p(xj) = Σ[j=1,N] p(z | xj) * wj % Teorema della probabilità assoluta
w(i+1) = p(xi | z) = p(z | xi) * p(xi) / Σ[j=1,N] p(z | xj) * wj
Così ad occhio mi sembrava un metodo molto elegante, anche perché nel calcolo di p(z | xj) è possibile usare una qualsiasi pdf e grazie alla sommatoria non è necessario normalizzare.
Fonte:
Nella prima consegna ho usato questo algoritmo con una normale di media 0 ed andavo a modulare la varianza in modo da avere risultati soddisfacenti.
Durante gli ultimi due incontri però, ho iniziato a chiedermi se questo metodo sia corretto e mi piacerebbe avere la sua opinione su di esso.
Ho provato anche ad utilizzare una mistura di gaussiane per il calcolo di p(z | xj) e, nel caso migliore, non ho ottenuto alcun miglioramento nelle performance del filtro.
2) Calcolo della distanza tra due coppie di punti in coordinate camera:
Per calcolare p(z | xj) ho usato la distanza tra i due punti (in coordinate camera) provenienti dalle misure e la pose della predizione, trasformata in coordinate camera.
Ho provato in due modi:
- Unendo le due coppie di punti in due vettori 4x1, facendo la differenza tra essi e poi prendendo la norma del vettore differenza (es. norm([4,9,5,7] - [3,9,6,2]))
- Prendendo la norma della differenza tra le due coppie di punti corrispondenti e poi sommando i due valori risultanti (es. norm([4,9]-[3,9]) + norm([5,7] - [6,2]))
Ho ottenuto risultati leggermente migliori con il secondo metodo e questo mi porta a pensare che ce ne possano essere altri.
Vorrei sapere se c'è un metodo preferibile per ottenere questa informazione.
3) Aggiunta del rumore sulle misure:
Le avevo parlato del problema che le particelle si condensavano sopra ad un unico stato a lezione ed ho già risolto quel problema sommando del rumore gaussiano (con matrice di covarianza specificata) alla predizione.
Mi è sembrato che si fosse detto anche di aggiungere del rumore alle misure, come abbiamo fatto con Kalman. (purtroppo, ho una pessima memoria e di questa cosa non ne sono sicuro al 100%)
Ho provato a farlo ed ho ottenuto risultati terribili, non importa come cambiassi i valori della matrice covarianza.
Ha quindi senso aggiungere del rumore alle misure (che in teoria sono già rumorose)?
4) Scrivendo il punto 3, mi è venuto in mente che anche durante lo sviluppo dell 'assignment sul filtro di Kalman, la matrice Q (4x4) non avesse un grosso impatto sull'output del filtro.
È possibile che ci sia un problema con le mie formule? Le ho controllate e confrontate più volte con quelle di Lisa, ma suppongo che sia possibile che abbiamo sbagliato entrambi.
Potrebbe essere causato da altro?
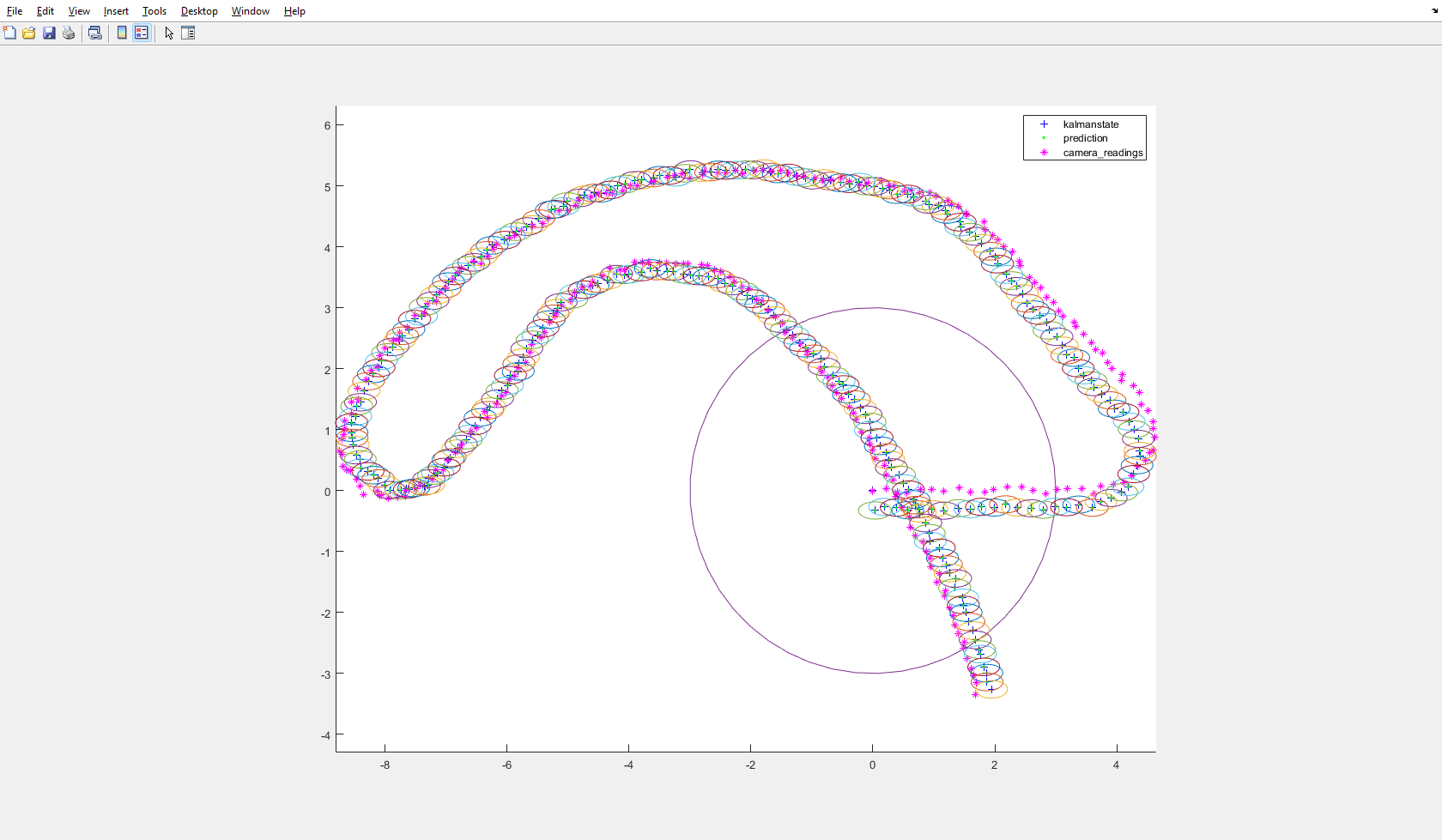
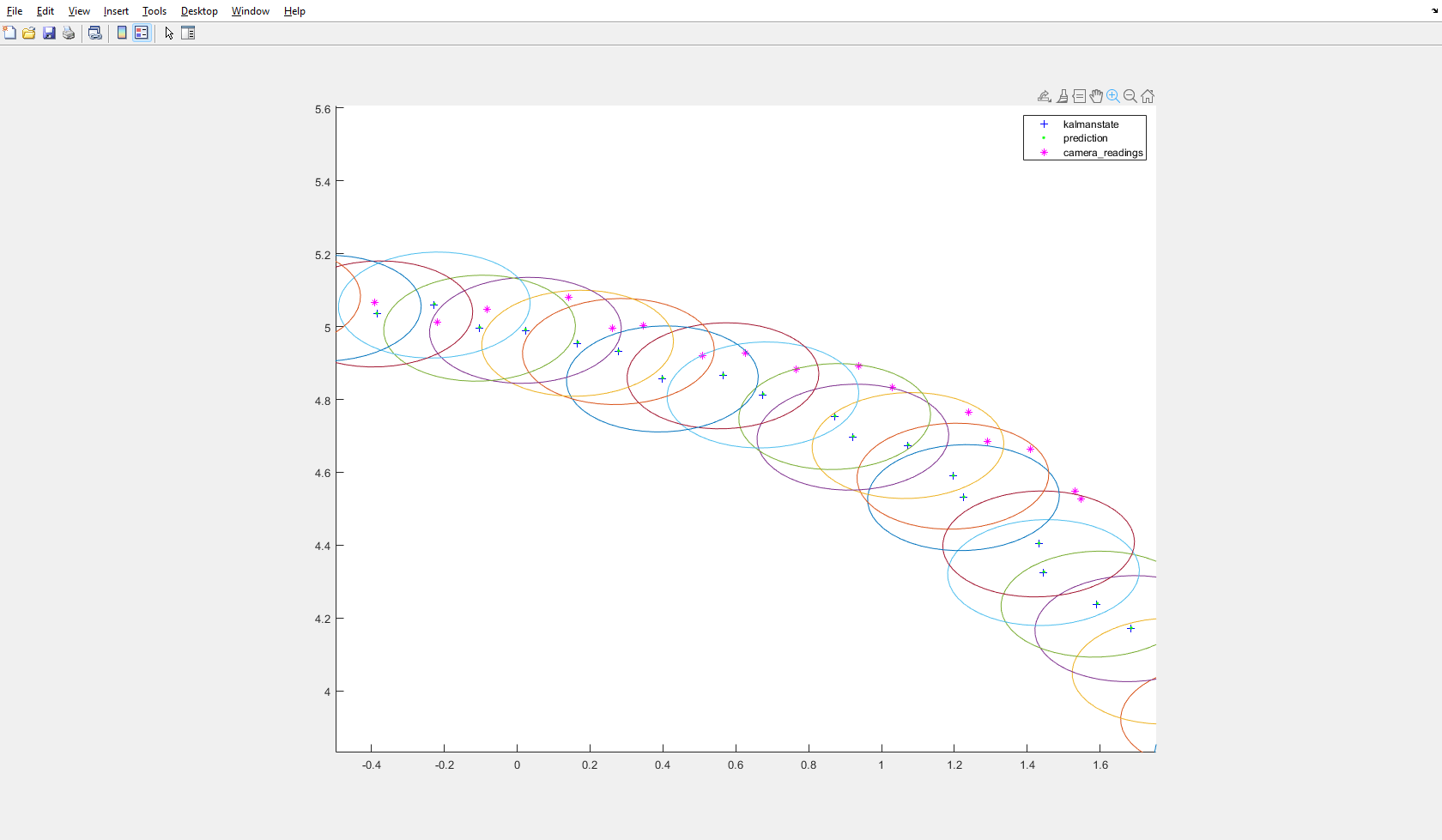
Questo è l'output del mio esercizio su KF in questo momento:
Lo stato del filtro sembra preferire di molto la predizione alle misure. Precedentemente mi sembrava normale, ma a questo punto ho paura di aver sbagliato qualcosa.